
连通图的最小生成树
生成树定义:
无向连通图G的极小连通子图,称为它的生成树。(n个顶点,n-1条边)
考虑一下下面这个图
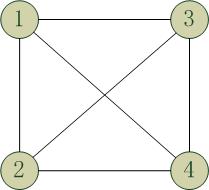
上图是一个完全图,它的生成树不是唯一的,我们列出最特殊的两种情况
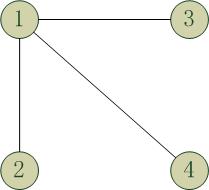
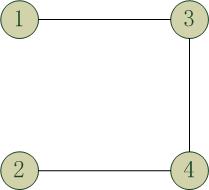
上面2个图都是第一个完全图的生成树,但是2者是完全不同的。
按照深度优先遍历生成的生成树,称为深度优先生成树
按照广度优先遍历生成的生成树,称为广度优先生成树
非连通图的生成森林,概念比较简单,无非就是非连通图的极大连通子图和生成树的概念叠加
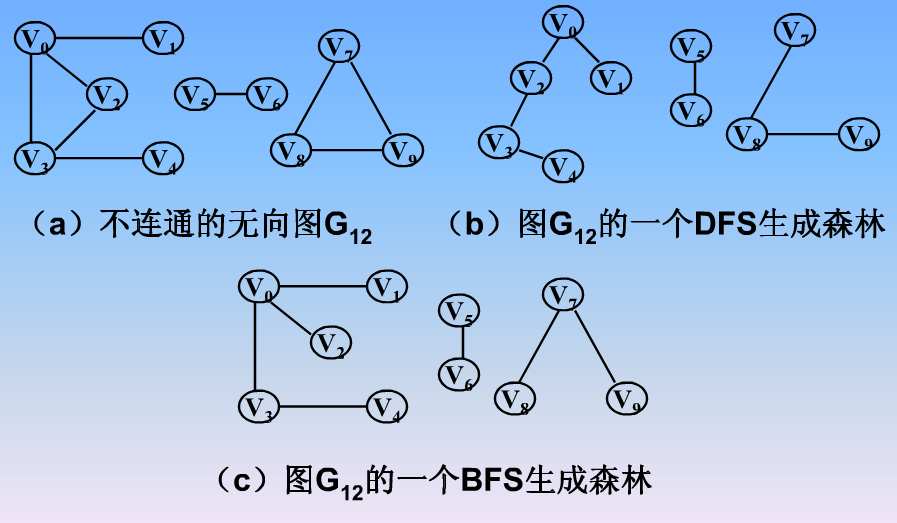
最小生成树
图G是带权的无向连通图,生成树上个边权值之和称为生成树的代价,代价最小的生成树称为最小生成树。
最小生成树的生成算法
Prim算法
现有连通图G=(V, E),其最小连通图TG=(TV, TE)。
初始状态下:V = {V0, V1, V2 ... Vn}; TV = {}
从V当中任选一顶点,插入TV,V = {V0, V1, V2 ... Vn}; TV = {V0}
找连接TV和V-TV这两个集合的权值最小的边,插入TE,并把该边2顶点当中原本不属于TV的顶点加入TV;
重复上一步骤
知道V = TV
下面是java实现,首先我们需要修改一下之前的生成图的代码,我们生成了一棵7个顶点的完全图,每一条边的权值是100以内的随机数。
Graph graph = new Graph();
String nodeNames[] = {"aaa", "bbb", "ccc", "ddd", "eee", "fff", "ggg"}; for (String s : nodeNames) { graph.nodes.add(new Node(s)); }graph.arcs = new int[nodeNames.length][nodeNames.length];
Random ra = new Random();
for (int i = 0; i < graph.nodes.size(); i ++){ for (int j = 0; j < graph.nodes.size(); j ++){ if (i != j){ graph.arcs[i][j] = ra.nextInt(100) + 1; } } }然后是最小生成树的Prim算法实现,解释一下,首先创建一个二维数组表示边,把空间都分配好,只等着往里面填数就行。然后是一个TreeMap对象,来保存顶点,之所以用TreeMap,是为了保证新图的顶点顺序和原图是一致的。剩下的基本就是跟前面算法描述的差不多,大家对着看就行,没什么太难的地方。
public Graph getMinTree(){
int newArcs[][] = new int[this.nodes.size()][this.nodes.size()]; Map<Integer, Node> newNodes = new TreeMap<Integer, Node>();newNodes.put(0, this.nodes.get(0));
while(newNodes.size() != this.nodes.size()){
int minWeight = 99999; int minI = -1; int minJ = -1; for(int i : newNodes.keySet()){ for (int j = 0; j < this.nodes.size(); j ++){ if (i != j && !newNodes.containsKey(j)){ if (this.arcs[i][j] < minWeight){ minWeight = this.arcs[i][j]; minI = i; minJ = j; } } } }newNodes.put(minJ, this.nodes.get(minJ));
newArcs[minI][minJ] = minWeight;newArcs[minJ][minI] = minWeight;
}Graph res = new Graph();
res.arcs = newArcs; res.nodes.addAll(newNodes.values()); return res; }下面有一次测试的输出,2个图,分别是原图的所有权值信息,另一个是最小生成树的权值信息
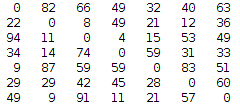
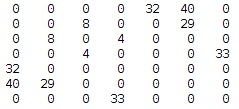
然后还可以用连通图的dfs算法检查一下。
Kruskal算法
先将所有边按照权值,从小到大排序
依次访问各边,如果生成回路,则舍弃,否则加入生成树,同时将该边的另一顶点加入生成树
直到所有顶点被加入
java实现,省略。